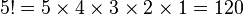The I Ching in 8 Bytes: 00000010010001010100001101001100101101100011101011 10011110111111

I really like the idea of this circular sequence as the whole of the I Ching, a 64 bit number which I stumbled upon tonight while looking for visual mappings of the hexagrams to binary numbers.
http://www.onlineclarity.co.uk/friends/showthread.php?t=5212
So from left ro right, 000000 is the hexagram kūn, Earth, the receptive:
_ _
_ _
_ _






image from http://proporzionedivina.blogspot.com/2009/06/i-ching-as-binary-system.html


00000010010001010100001101001100101101100011101011 10011110111111
6*64 = 384 lines to represent the entire realm of change...

Nice data visualisation

http://www.webdesignerdepot.com/2009/06/50-great-examples-of-data-visualization/

Simple visual version of Bubble Sort

Simple visual version of Bubble Sort, adapted from previous code
<----void draw() {


// If the mouse is pressed sort the array
if (mousePressed == true) {
bubbleSort(myArray);
for(int i=0;i fill(myArray[i]*20, myArray[i]*25, myArray[i]*5, myArray[i]*20);
ellipse(50, +i*25, myArray[i]*2, myArray[i]*2);
print(" " + myArray[i]);
}
}
}
------>

Bubble Sort algorithm

Nice bubble sort example from Kevin, I've made a simpler version below
/*
demonstrates a bubble sort algorithm, a variety of 'comparison sort'.
involves repeatedly stepping through the list to be sorted, comparing each pair of adjacent
items and swapping them if they are in the wrong order. The pass through the list is
repeated until no swaps are needed, which indicates that the list is sorted.
The algorithm gets its name from the way smaller elements "bubble" to the top of the list
adapted from Kevin:
http://processing.org/discourse/yabb/YaBB.cgi?board=Programs;action=display;num=1059766998

**/

//NASTY BLOG DOESNT WANT TO DISPLAY CODE PROPERLY

void bubbleSort(int array[])
{
int i, j;
boolean sorted = false;

// while the array isn't sorted
while (!sorted) {
sorted = true;
// loop through array
for (i=0;i array[i+1]) {
// swap values
j = array[i];
array[i] = array[i+1];
array[i+1] = j;
//println(array);
// trigger's been hit, array isn't sorted.
sorted = false;
}
}
}
}

Factorials: 5 ! = 5 * 4 *3 *2 * 1 = 120 \

(! means factorial) The factorial function (symbol: !) means to multiply a series of descending natural numbers. Can be used to find permutations and combinations, especially of large numbers

Here first 20 factorials:

void setup() {

for(int i=0;i<20;i++) {
long N = i;
println(i+ " :" +factorial(N));
}
}

long factorial(long n) {
if (n < 0) throw new RuntimeException("Underflow error in factorial");
else if (n > 20) throw new RuntimeException("Overflow error in factorial");
else if (n == 0) return 1;
else return n * factorial(n-1);
}

//Processing variation adapted from http://introcs.cs.princeton.edu/java/23recursion/Factorial.java.html

Output from code:

0 :1
1 :1
2 :2
3 :6
4 :24
5 :120
6 :720
7 :5040
8 :40320
9 :362880
10 :3628800
11 :39916800
12 :479001600
13 :6227020800
14 :87178291200
15 :1307674368000
16 :20922789888000
17 :355687428096000
18 :6402373705728000
19 :121645100408832000

Find prime numbers/prime factors

simple algorithm to find prime numbers and prime factors
depending on the value of N

void setup() {
long N =463;
for (long i = 2 ; i <= N ; i++) {
while (N % i == 0) {
System.out.println(i);
N = N/i;
}
}
}

Heron of Alexandria/Babylonian Algorithm to find square roots

imperative programming :
'imperative programs define sequences of commands for the computer to perform.'

Heron of Alexandria/Babylonian Algorithm to find the square root of a number, 3 versions here:

/*
1. Start with an initial guess (g) of what the square root of some number
(call it n) might be. The initial guess doesn't even have to be close. For simplicity's sake, let's always choose g = 1.
2. Compute result = ((n/g) + g)/2. Let g be the result just computed.
3. Repeat step 2 until the last two results obtained are the same.
sucessive approximation? Adapted from some C++ code I found on the web
*/

void setup() {
}
void draw() {

//doesn't really need to be in draw()

heronSqrt(44);
}

double heronSqrt(int number) {

double x = number/2;
for (int i = 0; i< 10; i++) {
x = (x + number/x)*0.5; //0.5
println("next approximate: " +x);
}
println("Processing guess: " + sqrt(number));
return x;
}
}

////another 2 variants:

//heron 2
void setup() {
heronTwo(44);
println(" ");
println(heron3(44));
}


double heronTwo(int n) {


double guess = n/2;
double r = 0.00;
for(int i = 0; i < 10; i++)
{
r = n / guess;
guess = (guess + r) / 2;
System.out.println(guess);
}

System.out.println("The square root of "+n+" is:");
System.out.printf(" [ %4.2f ]", r);//printf = formatted according to flags

return r;
}


double heron3(double number)

{ //square root Babylonian method



double estimate=number;

double divisor=2;

//below 100 is arbitrary, for very small decimals i values must be large

for(int i=0; i<100; i++)

{

estimate=number/divisor;

estimate=(estimate+divisor)/2; //find average estimate & divisor

divisor=estimate;
}

return estimate;
}